(JAVA) TreeMap은 어떻게 동작하는가?

이전 포스팅에서 레드 블랙트리에 대해서 포스팅하였다. TreeMap은 레드 블랙트리로 구성되어있다고 하는데 실제 구현 코드를 보면서 완전하게 이해하고자 합니다!
TreeMap은 레드 블랙트리를 사용하고 있다.
jwdeveloper.tistory.com/280?category=847363
(알고리즘) 레드블랙트리
이번 포스팅은 레드 블랙 트리를 포스팅할 예정이다. 레드 블랙트리를 포스팅하는 이유는 Java를 더 잘 이해하기 위해서이다. Java의 HashMap 사이즈가 64가 넘을 때에 레드 블랙트리를 사용하고 TreeM
jwdeveloper.tistory.com
이전에 포스팅한 내용을 기반으로 디버깅을 통해 구현원리를 살펴보자!
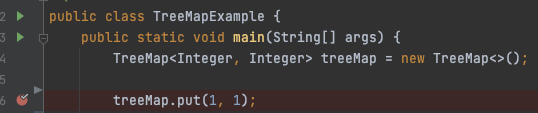
예시 코드는 아래와 같이 단순하다.
1, 65, 129, 193, 257, 257, 321, 385, 449, 513을 순차적으로 put 하는 코드이다.
첫 번째 put 인 1과
두 번째 put 인 65와
가장 복잡하였던 449를 기반으로 디버깅을 진행하겠습니다.
코드에 대한 내용을 포스팅할 것이기 때문에 레드 블랙트리에 대해 아직 원리를 모르시는 분은 위의 포스팅을 참고하시길 바랍니다!
예시 코드
/**
* Project : IntoJAVA
*
* @author : jwdeveloper
* @comment : TreeMap에 대해서
* Time : 12:12 오전
*/
public class TreeMapExample {
public static void main(String[] args) {
TreeMap<Integer, Integer> treeMap = new TreeMap<>();
treeMap.put(1, 1);
treeMap.put(65, 1);
treeMap.put(129, 1);
treeMap.put(193, 1);
treeMap.put(257, 1);
treeMap.put(321, 1);
treeMap.put(385, 1);
treeMap.put(449, 1);
treeMap.put(513, 1);
System.out.println(treeMap);
}
}
처음으로 데이터를 put 할 때
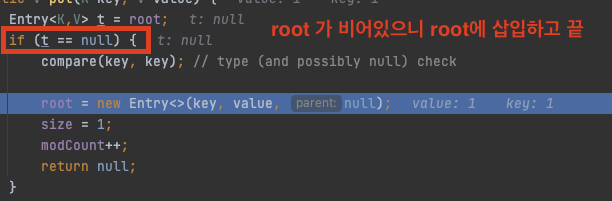
처음은 간단하다! 현재 root노드에 아무것도 없으니 현재 데이터를 root에 삽입하고 끝낸다.
Entry의 속성 값은 아래와 같이 key, value, "부모 노드"를 저장한다.
Entry(K key, V value, TreeMap.Entry<K,V> parent) {
this.key = key;
this.value = value;
this.parent = parent;
}65 삽입 시

root노드는 현재 가득 차있기 때문에 아래의 코드를 타게 된다.
현재 65는 root노드인 1보다 크기 때문에 오른쪽에 배치한다는 코드이다.
Entry<K,V> t = root; //root는 현재 [1, 1]
Entry<K,V> parent;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
왼, 오 를 설정한 이후에 아래와 같은 메서드로 향하게 된다.
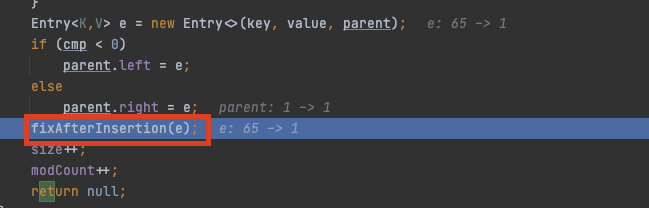
fixAfterInsertion은 삽입 노드를 red로 설정하고 Red-Red Violation이 일어났을 때를 처리하는 메서드이다.
현재는 부모 노드에 Black이니 Red-Red Violation 일어나지 않는다.
단순히 현재 노드를 red로 설정하고 끝낸다.
private void fixAfterInsertion(TreeMap.Entry<K,V> x) {
x.color = RED;
/*red-red violation 생략*/
root.color = BLACK;
}129 삽입 시
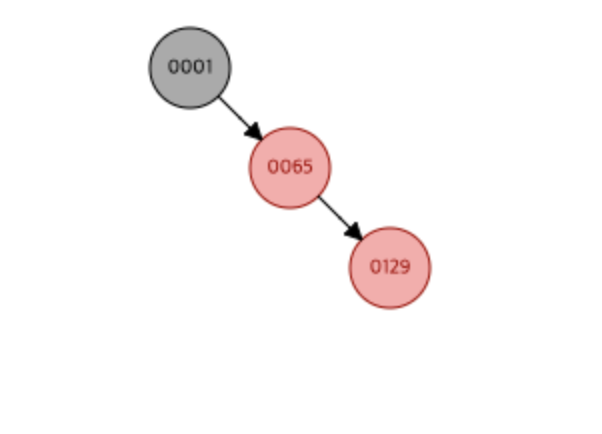
1 -> 65 -> 129 대소를 비교해서 오른쪽에 배치하는 것은 동어반복이 이기에 바로 fixAfterInsertion으로 들어가겠다.

현재 129는 부모 노드인 65와 Red-Red Violation이 일어난다.
아래와 같은 판단을 한다.
- 부모가 왼쪽인지 오른쪽인지 판단
- 삼촌과 부모가 같은 red 인지 판단
/*부모가 왼쪽인지 오른쪽인지 판단*/
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
}/*삼촌과 부모가 같은 red 인지 판단*/
Entry<K,V> y = leftOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
}
현재는 부모 노드가 오른쪽이고 삼촌 노드와 부모 노드가 red가 아니므로 해당사항이 없다.
아래의 메서드를 실행한다.
setColor로 부모의 노드를 black으로 조상의 노드를 red로 변경하고 왼쪽 회전을 한다.

왼쪽 회전
왼쪽 회전의 코드는 아래와 같다 코드가 난해하니 그림과 함께 살펴보도록 하겠다.
private void rotateLeft(TreeMap.Entry<K,V> p) {
if (p != null) {
TreeMap.Entry<K,V> r = p.right;
p.right = r.left;
if (r.left != null)
r.left.parent = p;
r.parent = p.parent;
if (p.parent == null)
root = r;
else if (p.parent.left == p)
p.parent.left = r;
else
p.parent.right = r;
r.left = p;
p.parent = r;
}
}
현재 상태
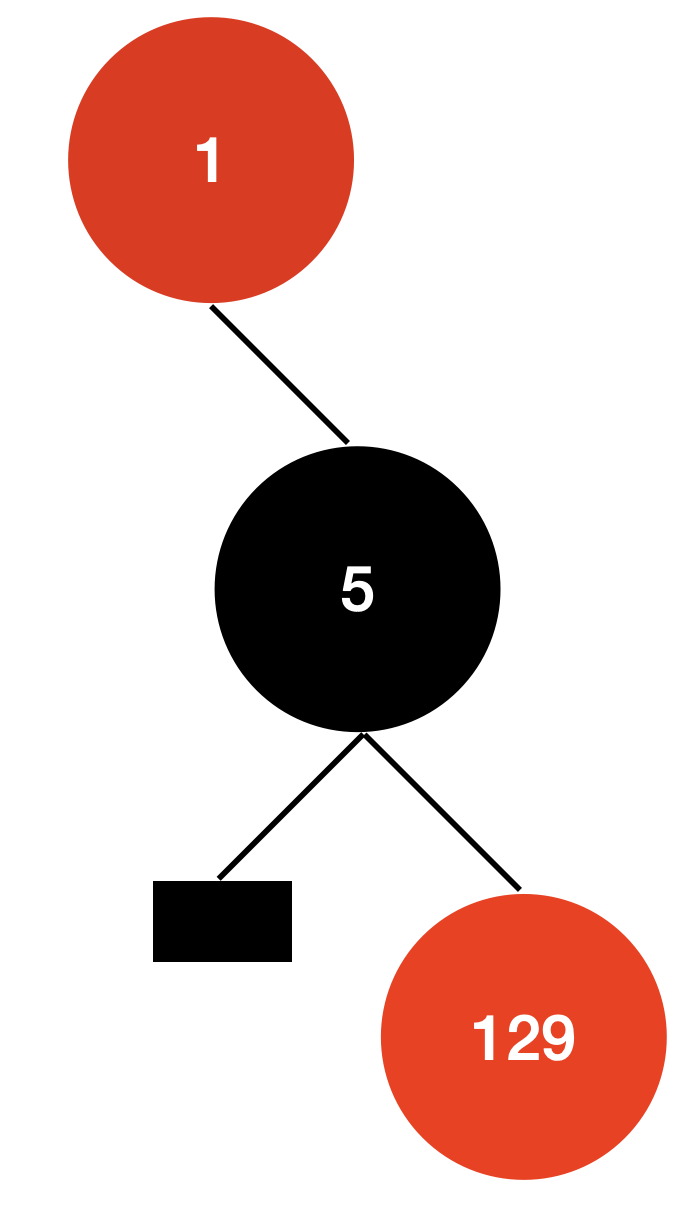
1. 할아버지 노드 (p), 부모 노드 (r) 설정하기
Entry<K,V> p // 현재 1
Entry<K,V> r = p.right;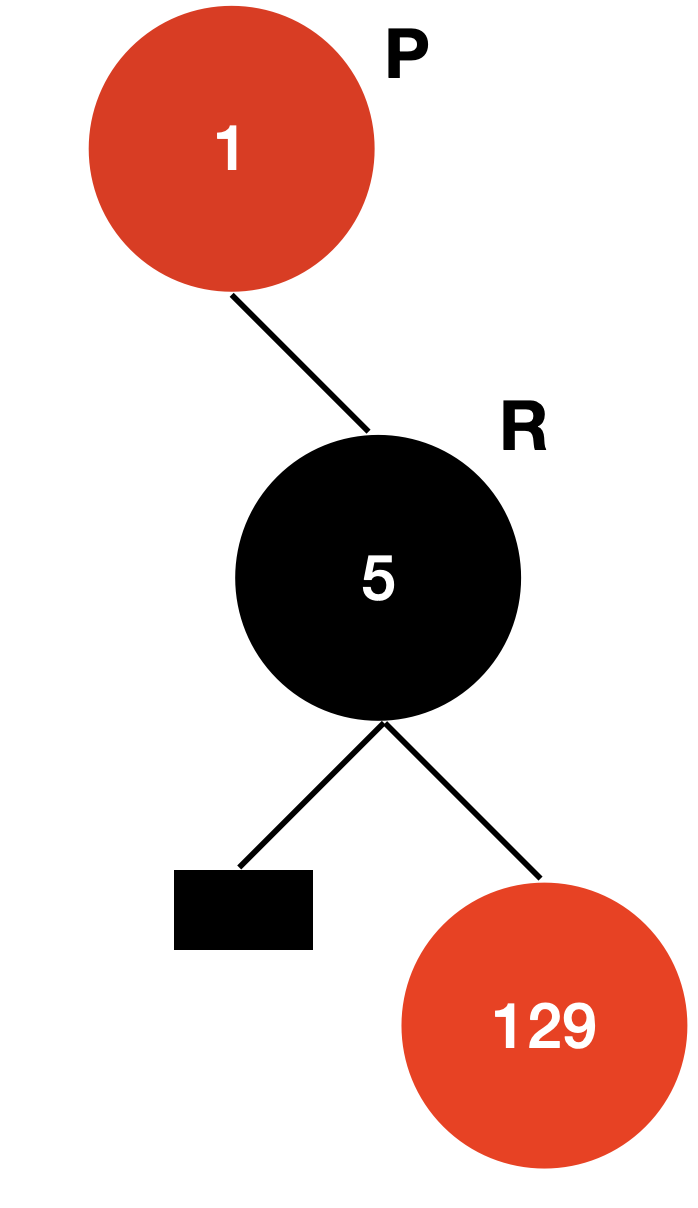
2. 부모 노드의 왼쪽 자식 할아버지 노드 오른쪽에 붙이기
현재 r의 왼쪽 노드는 없기 때문에 아래 과정은 skip 한다.
p.right = r.left; // 붙이고
if (r.left != null) // 끊어내는 작업
r.left.parent = p;
3. 할아버지 노드와 부모 노드 같은 부모 만들기
r.parent = p.parent;
4. 부모 노드를 할아버지 노드로 승격
if (p.parent == null)
root = r;
r.left = p;
p.parent = r;p의 조상 노드는 현재 없으므로 root를 r로 재설정하고 root인 r의 왼쪽을 p로 p의 부모를 r로 설정하면 아래와 같은 회전이 완성된다.
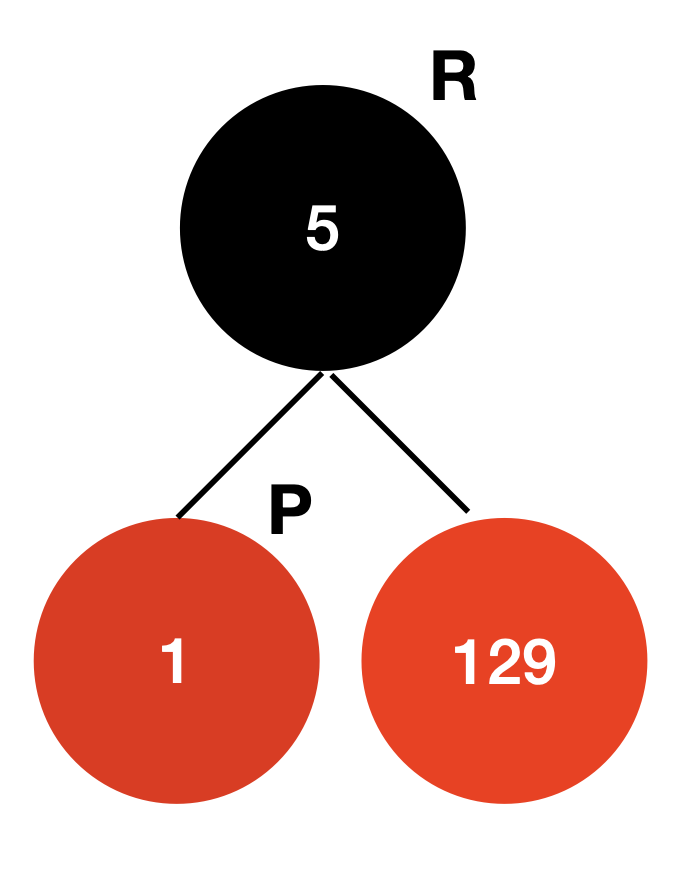
449 삽입 시
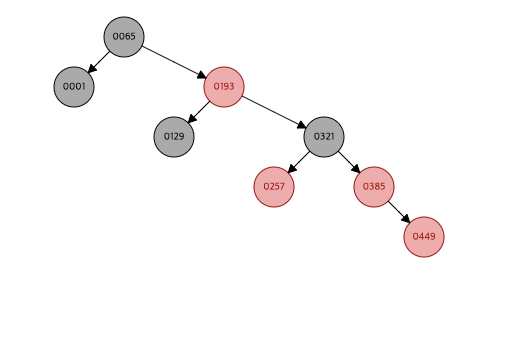
현재 삽입된 449와 385가 Red-Red Violation을 일으킨다.
while (x != null && x != root && x.parent.color == RED) {그러므로 해당 조건에 만족하여 루프를 타게 된다.
아래와 같은 판단을 한다.
1. 부모가 왼쪽인지 오른쪽인지 판단 -> 현재 오른쪽
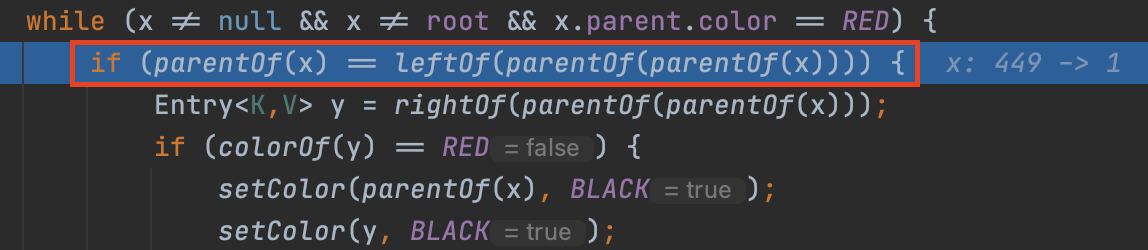
2. 삼촌과 부모가 같은 red 인지 판단 -> 삼촌과 부모가 같이 red

삼촌과 부모가 같은 red이기에 부모와 삼촌을 black으로 설정하고 할아버지를 red로 칠한다.
- 처리 후 대상을 다시 할아버지인 321로 설정한다.
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
321과 193의 Red-Red Violation
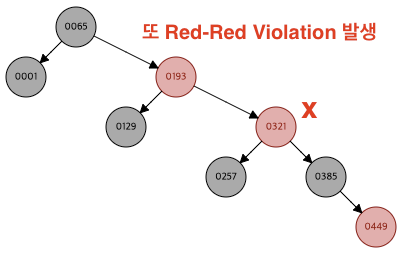
또 판단을 해야 한다.
1. 부모가 왼쪽인지 오른쪽인지 판단 -> 현재 오른쪽
2. 삼촌과 부모가 같은 red 인지 판단 -> 삼촌과 부모가 색이 다르다. 성립 X

왼쪽 회전
조상인 현재 root 노드 65를 기준으로 왼쪽 회전을 진행한다.
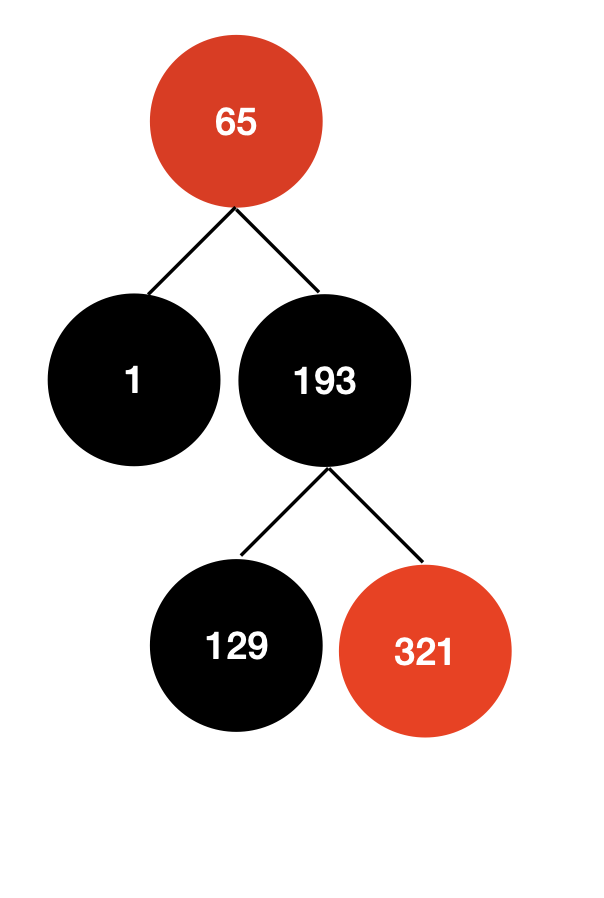
1. 할아버지 노드 (p), 부모 노드 (r) 설정하기
Entry<K,V> p // 현재 65
Entry<K,V> r = p.right;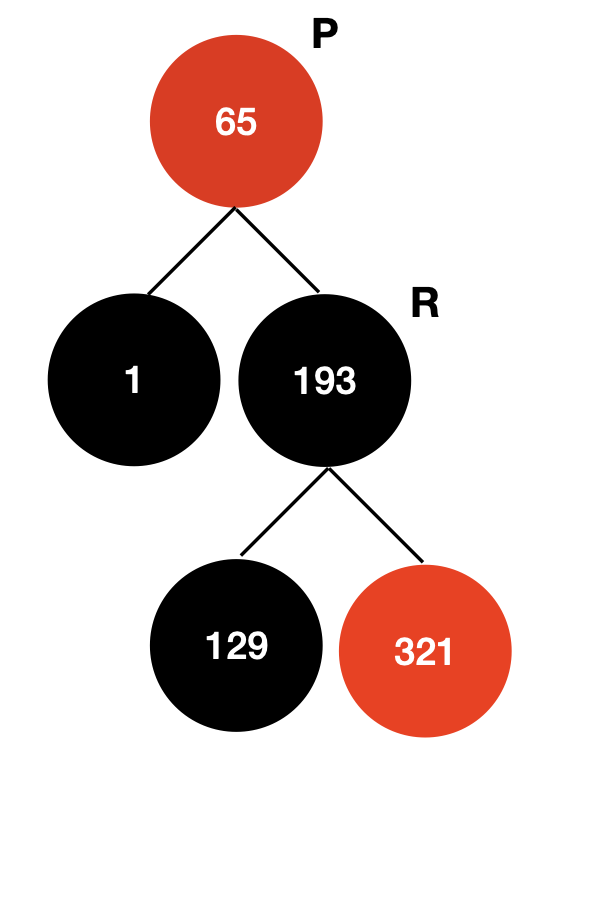
2. 부모 노드의 왼쪽 자식 할아버지 노드 오른쪽에 붙이기
p.right = r.left; // 붙이고
if (r.left != null) // 끊어내는 작업
r.left.parent = p;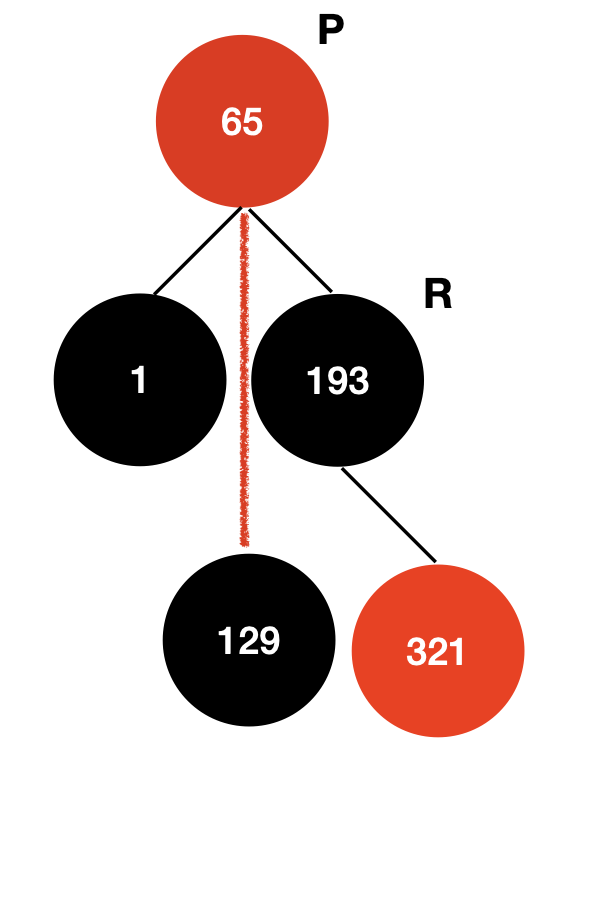
3. 할아버지 노드와 부모 노드 같은 부모 만들기
r.parent = p.parent;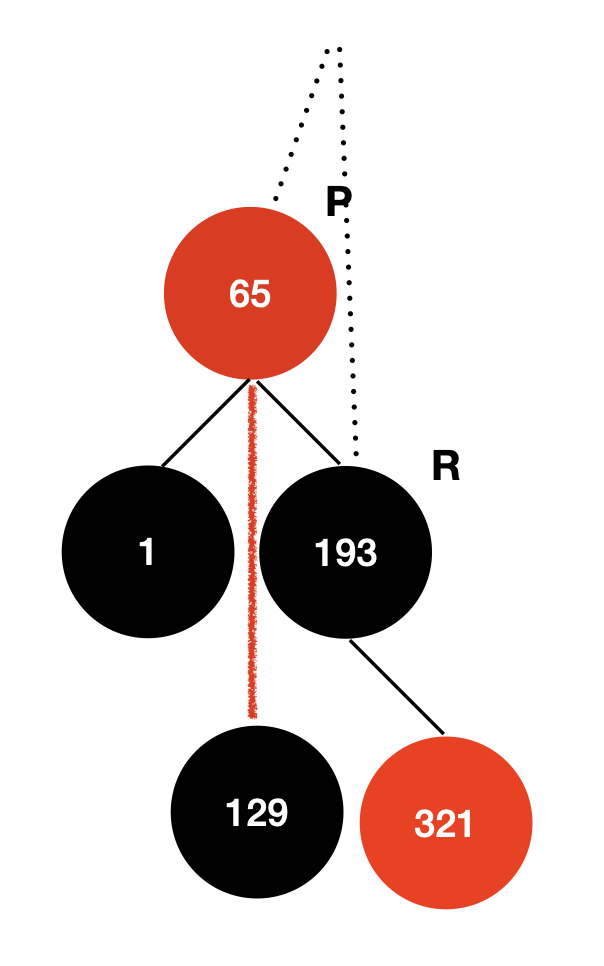
4. 부모 노드를 할아버지 노드로 승격
if (p.parent == null)
root = r;
r.left = p;
p.parent = r;
p의 조상 노드는 현재 없으므로 root를 r로 재설정하고 root인 r의 왼쪽을 p로 p의 부모를 r로 설정하면 아래와 같은 회전이 완성된다.
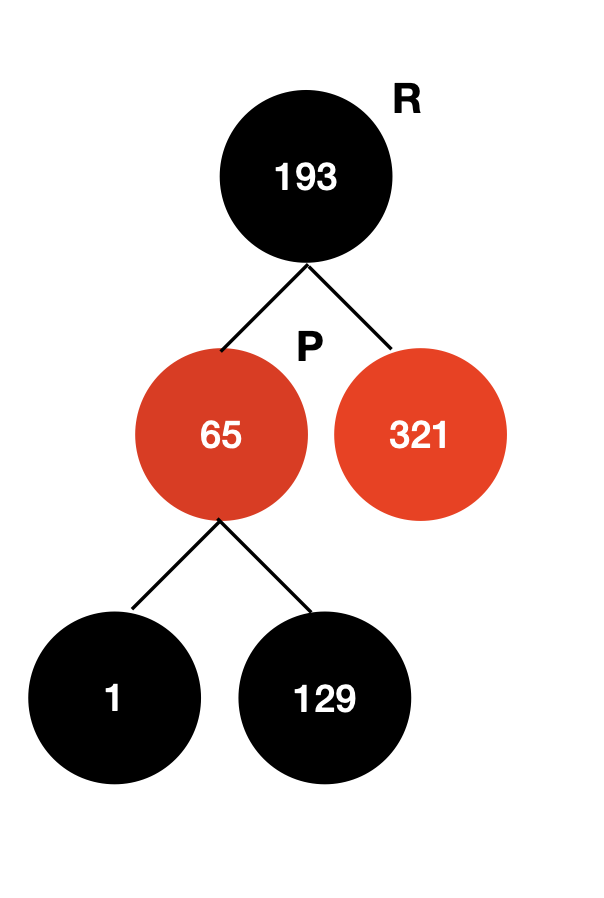
정리
현재 1, 65, 129, 193, 257, 257, 321, 385, 449, 513 값이 TreeMap에 어떻게 저장되는지 알아보았다.
모든 과정을 담을 수 도 있었지만 같은 과정의 반복이고 대표적으로 1. 65, 449 가 삽입돼는 과정을 중점적으로 알아보았다.
처음 레드 블랙트리 이론을 알고 나서는 약간 모호한 감이 있었지만 TreeMap을 통해서 내부를 살펴보지 확실하게 이해가 갔다.
제 블로그를 방문하는 몇몇의 분들에게 정확한 지식을 전달하려고 노력하였지만 잘못 이해하고 있는 부분이 있을 수도 있기에 피드백은 언제나 반갑게 받아들이겠습니다.
레드 블랙트리에 대한 이해에서부터 TreeMap의 삽입 과정까지... 험난한 과정이었지만 누군가 도움받을 수 있다는 생각을 하면 기부니가 좋습니다🥳